(上接第4题)(2)当点E在BA的延长线上时,如图3,点D在BC边上,且CE=DE,按照下面的操作,能够证明AE=BD的是( )
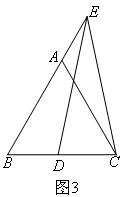
- A.直接证明△EAC≌△BDE
- B.①过点A作AF∥BC,交EC于点F;②△AEF是等边三角形;③△AFC≌△BDE
- C.①过点E作EF∥BC,交CA的延长线于点F;②△AEF是等边三角形;③△EFC≌△DBE
- D.①过点A作AF∥BC,交EC于点F,连接DF;②四边形FDBE是等腰梯形
答案
正确答案:C
知识点:类比探究
1.解题要点
此题中△ABC是等边三角形及CE=DE没有发生变化,所以可照搬(1)中的思路.
作辅助线;判断等边三角形(△AEF);证明△EFC≌△DBE.
作出的辅助线是:过点E作EF∥BC,交CA的延长线于点F.
2.解题过程
完整的证明过程如下:
如图,过点E作EF∥BC,交CA的延长线于点F.
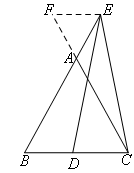
则∠AEF=∠B=∠EAF=∠BAC=60°,
∴△AEF是等边三角形,
∴AE=EF=AF,
∴BE=FC.
∵CE=DE,
∴∠EDC=∠ECD,
∴∠B+∠BED=∠ACB+∠FCE.
∵∠B=∠ACB,
∴∠BED=∠FCE,
∴△EFC≌△DBE(SAS),
∴EF=BD,
∴AE=BD.
略








