如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE,FE,则线段CE与EF之间的数量关系为( )

- A.CE=EF
- B.
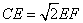
- C.
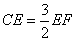
- D.
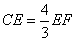
答案
正确答案:B
知识点:类比探究
(思路:从中点出发,由“直角+中点”想到直角三角形斜边中线等于斜边一半)
如图,连接CF.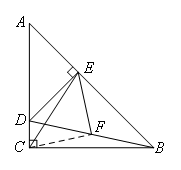
∵EF是Rt△BDE斜边上的中线,
∴EF=BF=DF,
∴∠DFE=2∠EBD.
∵CF是Rt△BCD斜边上的中线,
∴CF=BF=DF,
∴∠CFD=2∠CBF,CF=EF,
∴∠CFE=2(∠EBD+∠CBF)=2∠ABC=90°,
∴△CEF是等腰直角三角形,
∴![]() .
.
故选B.
略








