(上接第4,5题)如图,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,
以D为顶点作一个60°角,角的两边分别交AB,AC于E,F两点,连接EF,若BE=4,CF=2,则EF的值
为( )
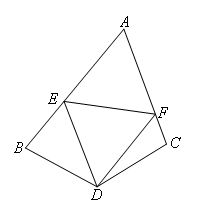
- A.7
- B.6
- C.5
- D.4
答案
正确答案:B
知识点:类比探究
(思路:此题无中点,无法类比倍长中线,但仔细观察前两题的做法,尤其是上一题,倍长中线相当于将△BDE绕点D顺时针旋转180°,结合本题条件,考虑将△BDE绕点D顺时针旋转120°.)
如图,延长AC至点G,使CG=BE,连接DG.
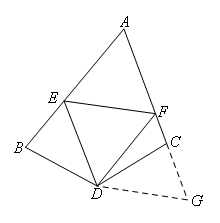
∵∠B+∠ACD=180°,∠DCG+∠ACD=180°,
∴∠B=∠DCG.
又∵DB=DC,
∴△BDE≌△CDG(SAS),
∴DE=DG,∠BDE=∠CDG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°,
∴∠CDG+∠CDF=60°,
即∠FDG=60°=∠FDE.
∵DF=DF,
∴△EDF≌△GDF(SAS),
∴EF=FG=FC+CG=FC+BE=6.
故选B.
略








