如图1,平面内有一等腰直角三角板ABC(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,则线段AF,BF,CE之间的数量关系为( )
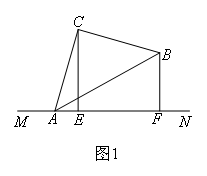
- A.AF=BF+CE
- B.AF-BF=2CE
- C.AF+BF=2CE
- D.
答案
正确答案:C
知识点:类比探究
(思路:看到“等线段共顶点”,想到旋转)
如图,过点C作CD⊥BF,交FB的延长线于点D.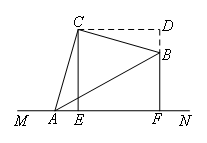
∵CE⊥MN,BF⊥MN,
∴CE∥DF,
∴∠DCE=90°.
又∵∠ACB=90°,
∴∠ACE=∠BCD.
∵AC=BC,
∴△ACE≌△BCD(AAS),
∴CE=CD,AE=BD,
∴四边形CEFD为正方形,
∴AF+BF=AE+EF+BF=2DF=2CE.
故选C.
略








