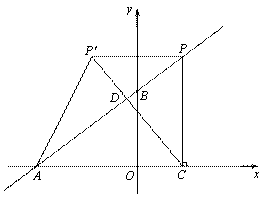
（2011浙江温州）如图，在平面直角坐标系中，O是坐标原点，点A的坐标为（-4，0），点B的坐标为（0，b）(b＞0)．P是直线AB上的一个动点，作PC⊥x轴，垂足为C，记点P关于y轴的对称点为P′ (点P′不在y轴上)，连结PP′，P′A，P′C，设点P的横坐标为a．
（1）当b=3时，①直线AB的解析式；②若点P′的坐标是（-1，m），求m的值；
（2）若点P在第一象限，记直线AB与P′C的交点为D．当P′D：DC=1：3时，求a的值；
（3）是否同时存在a，b，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．

解：（1）①设直线AB：y=kx+3把x=-4，y=0代入上式，解得k=∴
②由已知得点P（1，m）
∴m=，m=
（2）∵PP'∥AC
∴△PP'D∽△ACD∴，即∴
（3）以下分三种情况讨论①当点P在第一象限时：若∠A P'C=90°，P'A=P'C，如图1

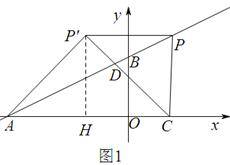
过点P'作P'H⊥x轴与点H
∴P P'=CH=AH= P'H=AC,
∴2a=（a+4）
∴a=
∵P'H=PC=AC，△ACP∽△AOB
∴，即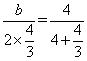，解得b=2.
若∠P′AC=90°，则AP′=AC，如图2，

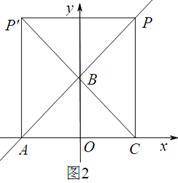
此时四边形ACPP′为正方形.
∴PP′=AC=CP=AP′
∴，
∴PP′=AC=CP=AP′=2a=8
∵△ACP∽△AOB
∴，即，解得b=4.
若∠P′CA=90°，则P′、P都在第一象限，与条件矛盾.
①点P在第二象限，则P′在第一象限，如图3，

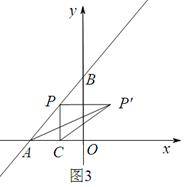
此时∠ACP′＞90°，矛盾.
②点P在第三象限，则P′在第四象限，如图4，

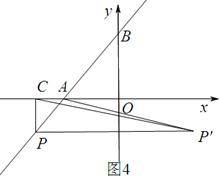
此时∠CAP′＞90°，矛盾.
综上所述，所有满足条件a，b的值为：或.

略