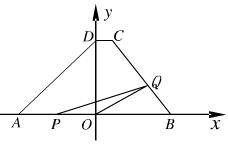
（2011山东烟台）如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上．直线CB的表达式为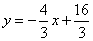
，点A、D的坐标分别为（－4，0），（0，4）．动点P自A点出发，在AB上匀速运动．动点Q自点B出发，在折线BCD上匀速运动，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）．
（1）求出点B、C的坐标；
（2）求S随t变化的函数关系式；
（3）当t为何值时S有最大值？并求出最大值．
，点A、D的坐标分别为（－4，0），（0，4）．动点P自A点出发，在AB上匀速运动．动点Q自点B出发，在折线BCD上匀速运动，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）．
答案
解：（1）把y＝4代入
，得x＝1.
∴C点的坐标为（1，4）.
当y＝0时，
，
∴x＝4.
∴点B坐标为（4，0）.
（2）作CM⊥AB于M，则CM＝4，BM＝3.
∴
.
∴sin∠ABC＝
＝
.
①0＜t＜4时，作QN⊥OB于N，则QN＝BQ·sin∠ABC＝t.
∴S＝
OP·QN＝
（4－t）×t＝
（0＜t＜4）.
②当4＜t≤5时，（如备用图1），
连接QO，QP，作QN⊥OB于N.同理可得QN＝t.
∴S＝OP·QN＝×（t－4）×t.＝
（4＜t≤5）.
③当5＜t≤6时，（如备用图2），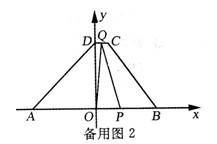
连接QO，QP.S＝×OP×OD＝（t－4）×4＝2t－8（5＜t≤6）.
（3）①在0＜t＜4时，当t＝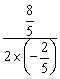
＝2时，S最大＝
＝
.
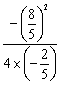②4＜t≤5时，对于抛物线S＝，当t＝－
＝2时，S最小＝
＝－.
∴抛物线S
＝的顶点为（2，－）.
∴在4＜t≤5时，S随t的增大而增大.
∴当t＝5时，S最大＝
＝2.
③在5＜t≤6时，在S＝2t－8中，
∵2＞0，
∴S随t的增大而增大.
∴当t＝6时，S最大＝2×6－8＝4.
∴综合三种情况，当t＝6时，S取得最大值，最大值是4.
（说明：（3）中的②也可以省略，但需要说明：在（2）中的②与③的△OPQ，③中的底边OP和高CD都大于②中的底边OP和高.所以③中的△OPQ面积一定大于②中的△OPQ的面积.）
知识点：中考压轴之动点问题
（1）把y=4代入，求得x的值，则可得点C的坐标，把y=0代入，求得x的值，即可得点B的坐标；
（2）作CM⊥AB于M，则可求得CM与BM的值，求得∠ABC的正弦值，然后分别从0＜t＜4时，当4＜t≤5时与当5＜t≤6时去分析求解即可求得答案；
（3）在（2）的情况下求S的最大值，然后比较即可求得答案.
略
WORD格式（
