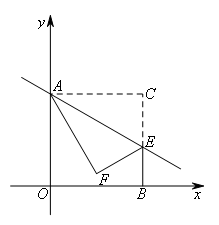
如图,在平面直角坐标系中,四边形AOBC是正方形,点A的坐标为(0,2),E是线段BC上一点,且∠AEC=60°,将正方形沿直线AE折叠,点C落在点F处,N是直线AE上一动点,若y轴上
存在点M,使得以点A,F,M,N为顶点的四边形是平行四边形,则点M的坐标为( )
- A.
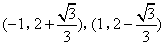
- B.
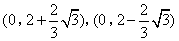
- C.
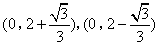
- D.
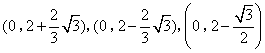
答案
正确答案:B
知识点:平行四边形的存在性
如图,过点F作FG⊥y轴于点G,
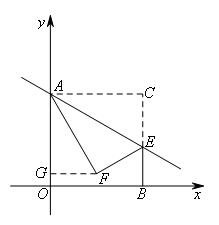
∵∠AEC=60°,
∴∠CAE=30°,
∴直线AE:![]() .
.
由折叠,得∠FAE=∠CAE=30°,AF=AC=OA=2,
∴∠GAF=30°,
∴GF=1,AG=![]() ,
,
∴![]() .
.
①当线段AF作平行四边形的边时,如图,

设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ;
;
设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ;
;
②当线段AF作平行四边形的对角线时,如图,

线段AF的中点坐标为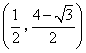 ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() .
.
综上,符合题意的点M的坐标为![]() .
.
故选B.
略








