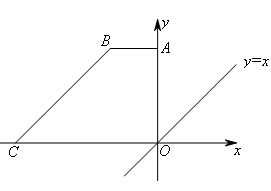
如图，在平面直角坐标系中，直角梯形OABC的边OC，OA分别在x轴、y轴上，AB∥OC，∠AOC=90°，∠BCO=45°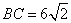，，点C的坐标为(-9，0)，点D在y轴上，点E在直线y=x轴上，若以O，B，D，E为顶点的四边形是平行四边形，则点D的坐标是(    )

       

如图，过点B作BF⊥x轴于点F，

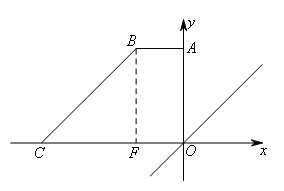
由题意得，C(-9，0)，
在Rt△BCF中，∠BCO=45°，，
∴BF=CF=6，OF=3
∴B(-3，6)．
若以O，B，D，E为顶点的四边形是平行四边形，则
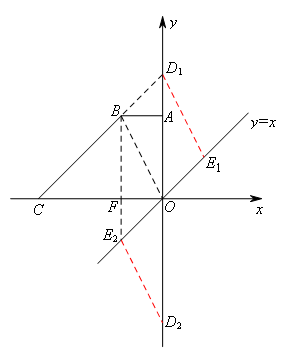
①当线段OB为边时，OB∥DE，OB=DE，如图所示：

设，则，则，∴，∴；
设，则，则，∴，∴；
②当线段OB为对角线时，DE与OB互相平分，如图：

取OB的中点，
设点，则，
∴，
∴，
∴与重合；
综上，符合题意的点D的坐标为(0，9)或(0，-9)．

略