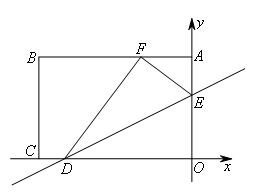
如图,将矩形OABC放置在平面直角坐标系中,OA=8,OC=12,直线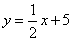 与x轴交于点D,与y轴交于点E,把矩形沿直线DE翻折,点O恰好落在AB边上的点F处,M是直线DE上的一个动点,点N在直线DF上,使四边形CDMN是平行四边形.则符合题意的点N的坐标( )
与x轴交于点D,与y轴交于点E,把矩形沿直线DE翻折,点O恰好落在AB边上的点F处,M是直线DE上的一个动点,点N在直线DF上,使四边形CDMN是平行四边形.则符合题意的点N的坐标( )
- A.
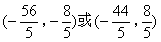
- B.
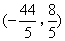
- C.
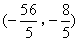
- D.
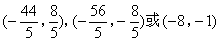
答案
正确答案:B
知识点:平行四边形的存在性
1.解题要点
①理解题意、整合信息.

②分析特征,有序思考,设计方案.
分析定点、动点:四边形CDMN是平行四边形,其中,点C,D是定点,点M,N是动点;
确定分类标准:四边形CDMN是平行四边形,顺序固定,此时定线段CD只能作为边,且位置固定.
③根据方案作出图形,有序操作.
四边形CDMN的顺序固定,根据题意,向上平移线段CD,使MN=CD=2,画出符合题意的图形,如图所示:
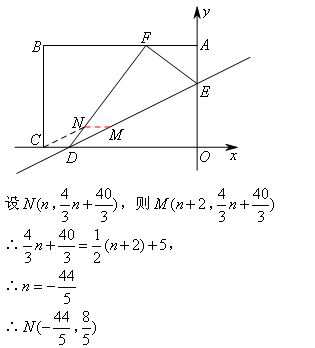
④检查验证.
作图验证;分析数据,估算验证.
2.解题过程
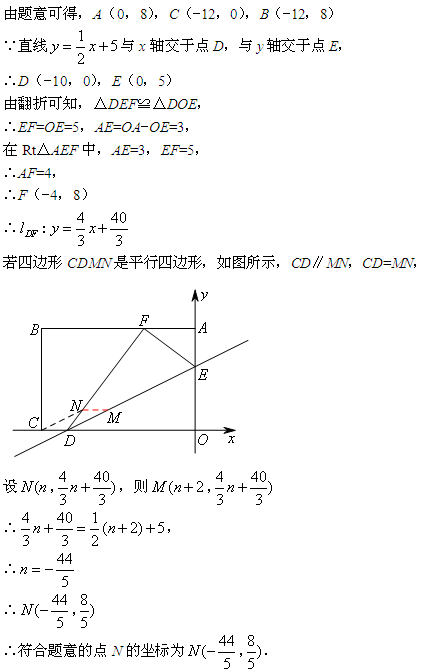
略








