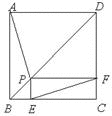
如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：
①AP =EF；
②AP⊥EF；
③△APD一定是等腰三角形；
④∠PFE=∠BAP；
⑤PD= EC．
其中正确结论的序号是_______

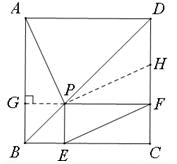
过P作PG⊥AB于点G，过P做PH∥EF
∵点P是正方形ABCD的对角线BD上一点，PE⊥BC，PG⊥AB
∴BEPG为正方形，BP为对角线
在△GPB中，∠GPB=45°，GB=GP=PE=BE，
∵AB=BC=GF，
∴AG=AB-GB，FP=GF-GP=AB-GB，
∴AG=PF，
∴△AGP≌△FPE，
∴AP=EF (①正确)
∴∠PFE=∠BAP (④正确)
PH∥EF，
所以∠PFE=∠FPH=∠BAP
故有∠BAP+∠APG=∠FPH+∠APG=90°
因为GF为平角，所以∠APH=90°，
AP⊥EF(②正确)
∵GF‖BC，
∴∠DPF=∠DBC，
又∵∠DPF=∠DBC=45°，
∴∠PDF=∠DPF=45°，
∴PF=EC，
∴在Rt△DPF中，DP=PF
∴DP= EC(⑤正确)．
③若△APD是等腰三角形；
∠ADP=45°，P点为BD上动点，
∴∠DAP=∠APD；
∵AD∥GF，
∴∠DAP=∠APG=∠APD
∵∠DPF=45°
∴∠DPA=∠DAP=62.5°
∵P为BD上动点，∠APD不可能恒为62.5°
∴△APD不一定是等腰三角形，③错误；
∴其中正确结论的序号是①②④⑤

拿题后没有一个命题一个命题的判断，思维受阻。几何类多命题判断题，命题的排列是有一定顺序的，从前到后有一定的联系，在读题判断中发现命题间的联系，是突破此类题目的关键。