已知：如图，EG平分∠BEF，FG平分∠EFD，∠1+∠2=90°．
求证：AB∥CD．

证明：如图，

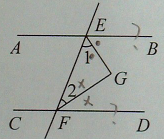
∵EG平分∠BEF（已知）
∴∠BEF=2∠1（角平分线的定义）
∵FG平分∠EFD（已知）
∴∠EFD=2∠2（角平分线的定义）
∵∠1+∠2=90°（已知）
∴2∠1+2∠2=180°（                    ）
∴∠BEF+∠EFD=180°（等量代换）
∴AB∥CD（                    ）
①等式性质；②平角的定义；③同旁内角互补；④两直线平行，同旁内角互补；
⑤同旁内角互补，两直线平行．
以上空缺处依次所填正确的是(    )

要证平行，想同位角，内错角，同旁内角，先从已知的条件出发，
由EG平分∠BEF，FG平分∠EFD，可以得到∠BEF+∠EFD=2∠1+2∠2，
结合∠1+∠2=90°，可知∠BEF+∠EFD=180°，
根据同旁内角互补，两直线平行得到AB∥CD．
第一个空：条件是∠1+∠2=90°，结论是2∠1+2∠2=180°，
是由等式∠1+∠2=90°两边同时乘以2得到，
因此理由是①等式的性质；
第二个空：条件是∠BEF+∠EFD=180°，
并且∠BEF和∠EFD是同旁内角，结论是AB∥CD，
由同旁内角互补得到两条直线平行，
理由是⑤同旁内角互补，两直线平行．
故选A．
想一想：要求一个角的度数，我们可以怎么考虑？
 
参考答案：首先观察图形，结合已知条件，看它可以看成什么角，然后设计方案求解．如果看成三角形的内角，可以考虑通过三角形的内角和等于180°求解；如果有平行，可以考虑通过平行转移角等等．

略