已知:如图,AB∥CD,∠1=110°,∠F=50°.求∠C的度数.
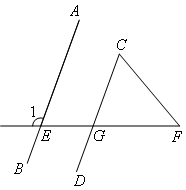
解:如图,
∵AB∥CD(已知)
∴∠1=∠CGE(两直线平行,同位角相等)
∵∠1=110°(已知)
∴∠CGE=110°(等量代换)
∵∠F=50°(已知)
∴∠C=∠CGE-∠F
=110°-50°
=60°(等式性质)
横线处应填写的过程恰当的是( )
- A.
∵∠CGE是△CGF的一个外角(外角的定义)
∴∠CGE=∠F+∠C(三角形的一个外角等于和它不相邻的两个内角的和) - B.
∵∠1是△CGF的一个外角(外角的定义)
∴∠1=∠F+∠C(三角形的一个外角等于和它不相邻的两个内角的和) - C.
∵∠CGE是△CGF的一个外角(外角的定义)
∴∠CGE=∠F+∠C(三角形的内角和是180°) - D.
∴∠C=60°(三角形的一个外角等于和它不相邻的两个内角的和)
答案
正确答案:A
如图,
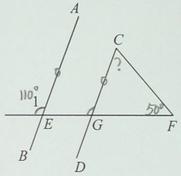
第一步:读题标注;
第二步:从条件出发,看到平行想同位角、内错角和同旁内角.
由AB∥CD得∠1=∠CGE,已知∠1=110°,等量代换,得∠CGE=110°.
∠CGE可以看作△CGF的一个外角,
根据三角形的一个外角等于和它不相邻的两个内角的和,得∠CGE=∠F+∠C,
又∠F=50°,利用等式性质,得∠C=∠CGE-∠F=110°-50°=60°.
本题给出的过程先是利用平行线的性质求∠CGE,再利用外角定理求出∠C.
故选A.
略








