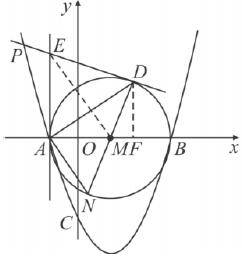
如图所示,抛物线与x轴交于点A(-1,0),B( 3,0)两点,与y轴交于点C( 0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN,AD.
(1)求抛物线所对应的函数关系式及抛物线的顶点坐标;
(2)若四边形EAMD的面积为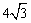 ,求直线PD的函数关系式;
,求直线PD的函数关系式;
(3)抛物线上是否存在点P,使得四边形EAMD的面积等于△DAN的面积?若存在,求出点P的坐标;若不存在,说明理由.
答案
(1)抛物线的函数关系式为:y = x2-2x-3,顶点坐标为( 1,-4).
(2)直线PD的函数关系式为y =-![]() x +
x +![]() 或y =
或y =![]() x-
x-![]()
( 3)故满足条件的点P的位置是4个,分别是:P1( 1+![]() ,2 ),P2(1-
,2 ),P2(1-![]() ,2 ),P3(1+
,2 ),P3(1+![]() ,-2 ),P4(1-
,-2 ),P4(1-![]() ,-2).
,-2).
知识点:中考压轴之圆
(1)抛物线经过点A(-1,0)、B( 3,0)、C( 0,-3),易求抛物线的函数关系式为:y = x2-2x-3,则顶点坐标为( 1,-4).
(2)连接EM
∵EA,ED是⊙M的两条切线
∴EA = ED,EA⊥AM,ED⊥MN∴△EAM≌△EDM.
又四边形EAMD的面积为![]() ,
,
∴S△EAM=![]()
∴![]() AM·AE =
AM·AE =![]() ,
,
又AM=2,∴AE=![]() .
.
因此,点E的坐标为E1(-1,![]() )或E2(-1,-
)或E2(-1,-![]() ).
).
当E点在第二象限时,切点D在第一象限.
在Rt△EAM中,tan∠EMA =![]() ,
,
∴∠EMA = 60°,∴∠DMB = 60°
过切点D作DF⊥AB,垂足为点F,
∴MF = 1,DF =![]() ,因此,切点D的坐标为( 2,
,因此,切点D的坐标为( 2,![]() ).
).
又由E(-1,![]() ),D( 2,
),D( 2,![]() )的坐标得
)的坐标得
直线PD的函数关系式为y =-![]() x +
x +![]() .
.


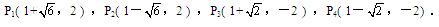
略








