如图，抛物线y＝x ²－6x＋8与x 轴交于A、B两点（点A在点B的左侧），直线y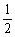＝x＋2交y轴于点C，且过点D（8，m）．左右平移抛物线y＝x ²－6x＋8，记平移后点A的对应点为A′，点B的对应点为B′．
（1）求线段AB、CD的长；
（2）当抛物线向右平移到某个位置时，A′D＋B′D最小，试确定此时抛物线的表达式；
（3）是否存在某个位置，使四边形A′B′DC的周长最小？若存在，求出此时抛物线的表达式和四边形A′B′DC的周长最小值；若不存在，请说明理由．

（1）令y＝x ²－6x＋8=0，解得x₁=2，x₂=4，由题意知A（2,0），B（4,0），则AB=2；
将D（8，m）代入直线表达式y＝x＋2，可计算出D点坐标为（8,6）；C点坐标为（0,2），过D作DE⊥y轴于点E，则DE=8，CE=4，在Rt△CDE中，由勾股定理知

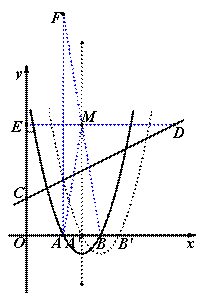
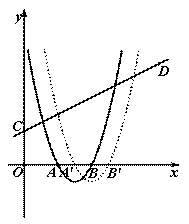
（2）类似于“奶站模型”：我们可以认为A、B两定点为居民区，动点M在直线DE上运动为送奶站，要确定M点的位置，保证AM+BM最小；然后把A、B、M三点连同奶站模型和抛物线一起向右平移，当M点与D点重合时，M点向右平移几个单位，说明抛物线向右平移几个单位，此时A、B分别与A′、B′重合，能保证A′D＋B′D最小。
使用奶站模型的处理思路可以确定M点的位置如上图，可以证明M点在抛物线的对称轴上，则DM=5，原抛物线的表达式为向右平移5个单位,则A′D＋B′D最小，抛物线的表达式为
（3）典型的天桥问题，等价于“A′、B′为x轴的两个动点，且A′B′=2，试确定A′、B′的坐标使得四边形A′B′DC的周长最小”

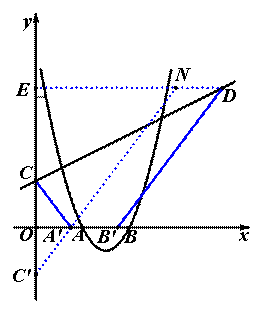
将点D向左平移两个单位到达N（6，6），则DN=A′B′=2，作C关于x轴的对称点C′，连结NC′交x轴于点A′，向右平移一个单位得到B′，连结CA′、DB′.因为NA′=DB′且根据奶站模型NA′+CA′最小，所以此时CA′+DB′最小.
C′（0，-2），N（6，6），则NC′所在直线为，该直线与x轴的交点坐标为，A′B′=2，则，则相当于原抛物线向左平移了个单位，抛物线的表达式为，此时四边形的周长最小，最小值为NC′+A′B′+CD=

略