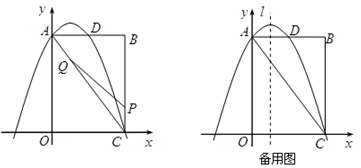
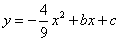如图，在矩形OABC中，点O为原点，点A的坐标为(0，8)，点C的坐标为(6，0)．抛物线经过点A、C，与AB交于点D．
（1）求抛物线的函数解析式；
（2）点P为线段BC上一个动点(不与点C重合)，点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．
①求S关于m的函数表达式；
②当S最大时，在抛物线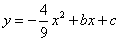的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

答案

解：（1）将A、C两点坐标代入抛物线，
解得抛物线的解析式为；
（2）①∵OA=8，OC=6
∴，
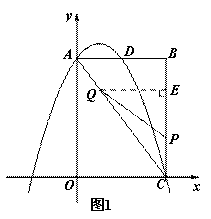
过点Q作QE⊥BC与E点，则，

∴，
∴，
∴
∴当m=5时，S取最大值；
②在抛物线对称轴l上存在点F，使△FDQ为直角三角形，满足条件的点F共有四个，坐标分别为
．

知识点：中考热点函数问题  

（1）将A、C两点坐标代入抛物线，即可求得抛物线的解析式；
（2）①过点Q作QE⊥BC于点E，则可利用相似或者利用sin∠ACB表示出QE的长度，进而求出三角形的面积S关于m的函数，化简为顶点式，便可求出S的最大值；
②首先由①得S取最大值时，m=5，即此时AQ=QC=5，Q为AC的中点，可得Q（3,4）．
又由D点纵坐标为8，可得D（3，8），可知DQ⊥x轴；
再由△DFQ为直角三角形，故需要分情况讨论：
若∠FDQ=90°，如图2，可知DF∥y轴，此时；

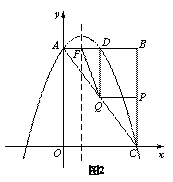
若∠DQF=90°，如图3，可知QF∥y轴，此时

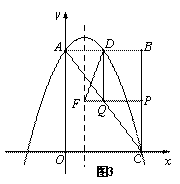
若∠DFQ=90°，此时相当于以DQ为直径作圆，圆与对称轴的交点即为F点，作QM⊥DQ交对称轴与点M，则利用常见的双垂直模型解决问题．此时：

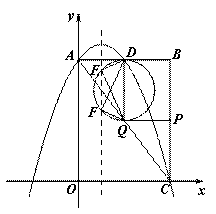
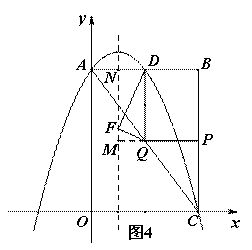
略

下载次数：17

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>