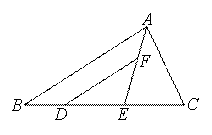
如图，在△ABC中，AB≠AC，D、E在BC上，且DE=EC，过D作DF∥BA交AE于点F，DF=AC.求证：AE平分∠BAC.
答案
延长AE至G，使EG=AE，连接DG.
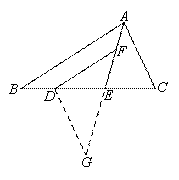
又∵DE=EC，∠AEC=∠GED，
∴△AEC≌△GED（SAS）
∴DG=AC，∠G=∠CAE
又∵DF=AC∴DF=DG
∴∠G=∠DFG
又∵DF∥BA
∴∠DFG=∠BAE∴
∠CAE=∠BAE，即AE平分∠BAC.
这道题目直接证明是证明不出来的，那么就需要添加辅助线，而辅助线的突破口就在于条件中的“DE=EC、DF=AC”，由DE=EC知，AE是隐含的△ACD的中线，那我们就可以通过倍长中线将AC等量转移到D点下方，使之能与DF构成一个等腰三角形。
略
WORD格式（
