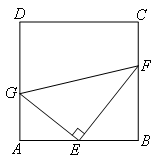
如图，在四边形ABCD中，AD∥BC，E为AB边的中点，G，F分别为AD，BC边上的点，
GE⊥EF，若AG=2，BF=3，则GF=(    )

要求GF的长，已知的是AG=2，BF=3，条件比较分散，
考虑作辅助线将条件集中，AD∥BC，E为AB边的中点，
这是平行夹中点结构，考虑倍长中线，如图：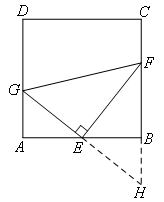

延长GE交FB的延长线于点H，可以证明△AEG≌△BEH（ASA），
可以得到：AG=BH，GE=HE，
又因为GE⊥EF，所以EF是线段GH的垂直平分线，
则GF=FH，FH=BF+BH=BF+AG=3+2=5，所以GF=5．
故选C．

略