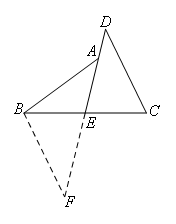
如图，点E是BC的中点，∠BAE＝∠D．某同学通过添加辅助线：延长DE到点F，使
EF=DE，连接BF．给出下列结论：①△BFE≌△CDE，②BF∥CD，③AB=CD，④AE=BE，其中一定正确的有(    )

如图：

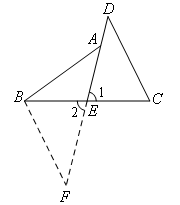
延长DE到点F使EF=DE，连接BF之后，由E是BC的中点，
可得BE=CE，结合对顶角∠2=∠1，可证△BFE≌△CDE（SAS），
由全等可以得到：∠F=∠D，BF=CD，
进而可以得到BF∥CD（内错角相等，两直线平行），
因为∠BAE=∠D，所以∠BAE=∠F，则AB=BF（等角对等边），
所以AB=CD，正确的结论为①②③．
故选A．

略