已知:如图,在四边形ABCD中,AD∥BC,点E是CD的中点,连接AE,BE,且AE⊥BE.求证:AB=AD+BC.

证明:如图,

∵AD∥BC
∴∠D=∠1
∵E是CD的中点
∴DE=CE
在△ADE和△FCE中

∴△ADE≌△FCE( )
∴
∵AE⊥BE
∴∠AEB=∠FEB=90°
在△AEB和△FEB中

∴△AEB≌△FEB( )
请你仔细观察下列序号所代表的内容:
①延长AE到F,使EF=AE,连接CF;②延长AE交BC的延长线于点F;
③ASA;④SAS;⑤AAS;⑥AE=FE;⑦AE=FE,AD=FC;
⑧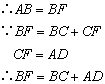 ;⑨
;⑨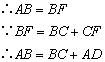 .
.
以上空缺处依次所填最恰当的是( )
- A.①⑤⑥③⑧
- B.②⑤⑦③⑨
- C.①⑤⑥④⑧
- D.②③⑦④⑨
答案
正确答案:D
知识点:全等三角形之截长补短
观察图形,这里有一个平行夹中点,
可以考虑延长AE交BC的延长线于点F,证得△ADE≌△FCE,
结合要证明的结论,通过证明△AEB≌△FEB得到AB=BF,即AB=AD+BC.
由AD∥BC得到∠D=∠1,E是CD的中点,则DE=CE,
结合对顶角相等可以证得△ADE≌△FCE(ASA);
由△ADE≌△FCE可得AE=FE,AD=FC,
结合AE⊥BE可以证得△AEB≌△FEB(SAS),由全等可以得到AB=FB,
进而得到AB=AD+BC.
空缺处依次所填最恰当的是②③⑦④⑨.
故选D.
略











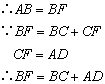 ;⑨
;⑨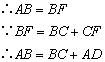 .
.