如图，在四边形ABCD中，AB∥CD，AD∥BC，AD=2CD，CE⊥AB于E，F为AD的中点，
若∠AEF=54°，则∠D=( )
- A.54°
- B.60°
- C.66°
- D.72°
答案
正确答案：D
知识点：全等三角形的性质与判定 直角三角形斜边中线等于斜边的一半 平行夹中点
如图，延长EF交CD的延长线于点G，连接FC．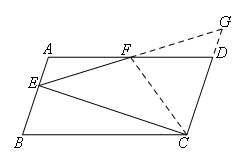
∵AB∥CD，
∴∠G=∠AEF=54°，∠A=∠GDF，
∵F为AD的中点，
∴AF=DF，
∴△AEF≌△DGF（AAS），
∴EF=GF，
∵CE⊥AB，AB∥CD
∴∠ECD=90°，
∴FC=EF=GF，
∴∠DCF=∠G=54°，
∵AD=2CD，
∴CD=DF，
∴∠CFD=54°，
∴∠CDF=72°．
故选D．
略
WORD格式（
