（上接第6题）如图3，在四边形ABCD中，AB=AD，E，F分别为DC，BC边上的点，且满足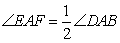，当∠ABC与∠ADC满足(    )时，可使得DE+BF=EF．

试题6中图1和图2的证明，都是利用旋转的思想来证明DE+BF=EF，
从作辅助线开始到结束，整个分析有以下几点：
延长CB到点G，使得BG=DE，证明△ABG≌△ADE（SAS），导出∠GAF=∠EAF，进而证明△GAF≌△EAF（SAS），之后导出线段关系．
若在图3中用此方法证明，首先延长CB到点G，使得BG=DE，要证明△ABG和△ADE全等，需要保证∠ABG=∠ADE，也就是需要∠ABC+∠ADC=180°，所以需要添加的条件是∠ABC+∠ADC=180°．
添加条件之后的证明如下：
如图，延长CB到点G，使得BG=DE，连接AG．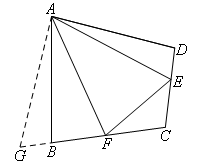

∵∠ABC+∠ADC=180°，∠ABC+∠ABG=180°，
∴∠ABG=∠ADE．
又∵AB=AD，BG=DE，
∴△ADE≌△ABG，
∴AE=AG，BG=DE，∠DAE=∠BAG，
∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF．
∵，
∴∠GAF=∠EAF．
又∵AF=AF，
∴△GAF≌△EAF，
∴GF=EF，
∴EF=GB+BF=DE+BF．
故选B．

略