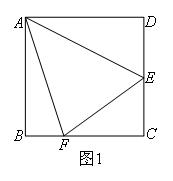
如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接
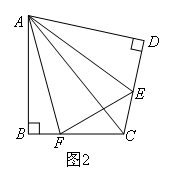
EF.利用旋转的思想很容易证明DE+BF=EF;如图2,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且 .则DE,BF,EF之间的数量关系为( )
.则DE,BF,EF之间的数量关系为( )
- A.
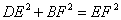
- B.
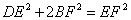
- C.
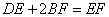
- D.
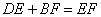
答案
正确答案:D
知识点:旋转的性质 三角形全等的判定及性质 类比探究问题
在图1中,旋转思想考虑了两个方面,一个是AB=AD,能够实现旋转,一个是![]() ,能够将角度放在一起,所以图1中的证明是将△DAE旋转,使得AD与AB重合,这是一种思想,作辅助线的时候是延长CB到点G,使得BG=DE,最后证明GF=EF.
,能够将角度放在一起,所以图1中的证明是将△DAE旋转,使得AD与AB重合,这是一种思想,作辅助线的时候是延长CB到点G,使得BG=DE,最后证明GF=EF.
图2中有同样的两个结构:AB=AD,![]() ,所以照搬分析图1的思路来研究数量关系.
,所以照搬分析图1的思路来研究数量关系.
如图,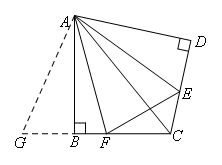
延长CB到点G,使得BG=DE,连接AG.
易证△ADE≌△ABG,
∴AE=AG,BG=DE,∠DAE=∠BAG,
∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF.
∵![]() ,
,
∴∠GAF=∠EAF.
又∵AF=AF,
∴△GAF≌△EAF,
∴GF=EF,
∴EF=GB+BF=DE+BF,
即DE,BF,EF满足的数量关系是DE+BF=EF.
故选D.
略









