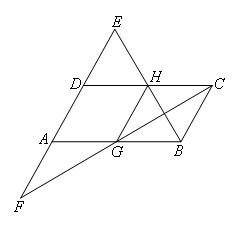
如图，在平行四边形ABCD中，AB=2AD，延长AD到E，反向延长AD到F，使DE=AD=AF．连接CF，交AB于点G，连接BE，交CD于点H，连接GH．则下列结论不一定正确的是(    )

如图，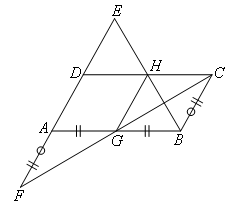

由AF=AD=BC，AF∥BC，可证△AFG≌△BCG，
则AG=BG=AB=AD，故AF=AG，△AFG是等腰三角形，选项A正确．

同理，DE=DH，△DEH是等腰三角形，选项B不一定正确．

由选项A中分析，同理可证△DEH≌△CBH，
则CH=CB=BG，又CH∥BG，可证四边形CHGB是菱形，选项C正确．

由选项C可得，四边形ADHG是菱形，
若AB⊥BC，则可得∠ABC=∠DAG=90°，
则四边形ADHG是正方形，选项D正确．
故选B

略