如图，在Rt△ABC中，∠ACB=90°，CF⊥AB于点F，BD平分∠ABC，且交CF于G，DE⊥AB于点E，则下列结论不一定正确的是(    )

如图，N，C，A三点在同一直线上，△ABC中，∠A：∠ABC：
∠ACB=3:5:10．若△MNC≌△ABC，则∠BCM的度数为(    )

已知△ABC的三边长分别为3，4，5，△DEF的三边长分别为3，3x-2，2x+1，若这两个三角形全等，则x的值为(    )

在△ABC中，AD⊥BC，D为BC的中点，则以下结论不正确的是(    )

已知：如图，在△ABC中，BD=CD，∠1=∠2．求证：AD是∠BAC的平分线．

①过D作DE⊥AB于E，DF⊥AC于F；
②∴DE=DF（全等三角形对应边相等）；
③∴∠BED=∠CFD=∠AED=∠AFD=90°；
④∴∠DAE=∠DAF（全等三角形对应角相等）
∴AD是∠BAC的平分线；
⑤延长CD交AB于E，延长BD交AC于F；
⑥在△BDE和△CDF中
；
⑦在Rt△ADE和Rt△ADF中
；
⑧在△ABD和△ACD中
．
下列证明过程正确的是(    )

已知：如图，点B，E，F，C在同一直线上，AB=DC，BE=CF，∠B=∠C．
求证：OA=OD．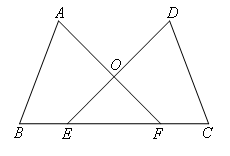

证明：如图，过点O作OG⊥EF于G．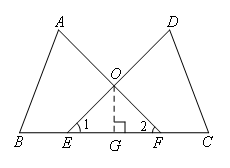

∵BE=CF
∴BE+EF=CF+EF
即BF=CE
在△ABF和△DCE中
                        
∴△ABF≌△DCE（     ）
∴∠2=∠1（全等三角形对应角相等）
AF=DE（全等三角形对应边相等）
∵OG⊥EF
∴∠OGE=∠OGF=90°
在△OEG和△OFG中
                        
∴△OEG≌△OFG（     ）
∴OE=OF（全等三角形对应边相等）
∴AF-OF=DE-OE
即OA=OD
请你仔细观察下列序号所代表的内容：
①；②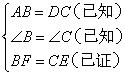；③SAS；④SSA；⑤ASA；
⑥AAS；⑦；⑧．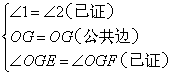
以上空缺处依次所填正确的是(    )

已知：如图，在四边形ABCD中，AD∥BC，AD=BC．
求证：∠A=∠C．

证明：如图，连接BD，

                         
在△ABD和△CDB中
                         
∴△ABD≌△CDB（     ）
∴∠A=∠C（全等三角形对应角相等）
请你仔细观察下列序号所代表的内容：
①；②；③；④；
⑤SAS；⑥SSA
以上空缺处依次所填正确的是(    )

已知：如图，AB=AC，ME⊥AB，MF⊥AC，垂足分别是E，F，ME=MF．
求证：MB=MC．

下列证明思路正确的是(    )

已知：如图，AB=AE，BC=DE，∠B=∠E，F是CD的中点．
求证：∠BAF=∠EAF．

下面是小明的几种思路，其中正确的是(    )

如图，在正方形ABCD中，∠ABC=∠BCD=90°，AB=BC=CD．E为BC边上一点，且AE=DE，AE与对角线BD交于点F，∠ABF=∠CBF，连接CF，交ED于点G．
求证：DE⊥CF．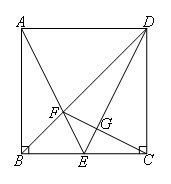

证明：如图，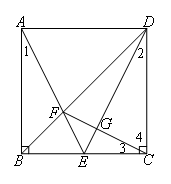

在Rt△ABE和Rt△DCE中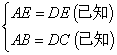

∴Rt△ABE≌Rt△DCE（HL）
∴                 
在△ABF与△CBF中
                 
∴               
∴               
∴∠2=∠3
∵∠BCD=90°
∴∠3+∠4=90°
∴∠2+∠4=90°
∴∠DGC=90°
∴DE⊥CF
请你仔细观察下列序号所代表的内容：
①∠1=∠2（全等三角形对应角相等）；②∠1=∠3（全等三角形对应角相等）；
③∠ABE=∠DEC（全等三角形对应角相等）；④；⑤；
⑥△ABF≌△CBF（SAS）；⑦△ABF≌△CBF（SSS）；⑧∠AFB=∠CFB（全等三角形对应角相等）．
以上空缺处依次所填正确的是(    )