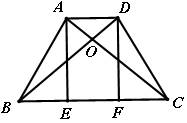
如图，在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD，AE⊥BC ，DF⊥BC，垂足分别为E、F，设AD=a，BC=b，则四边形AEFD的周长是（     ）

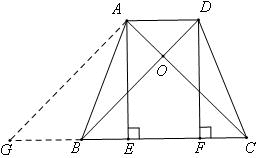
如图，过点A作DB的平行线交CB的延长线于点G，则四边形AGBD为平行四边形，所以GB＝AD＝a，GC＝GB＋BC＝a＋b，因为AC⊥BD，所以AC⊥AG，又因为四边形ABCD为等腰梯形，则易证△ABD≌△DCA，所以AC＝DB，故AC＝AG，即△AGC为等腰直角三角形，而AE⊥BC，所以AE为直角三角形AGC斜边GC的中线，因此AE＝＝.由题中的已知条件易判断四边形AEFD为长方形，所以四边形AEFD的周长C＝2AE＋2AD＝（a＋b）＋2a＝3a＋b.故答案为3a＋b.

不能借助合适的辅助线进行有效的解题