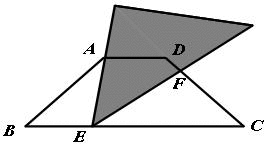
如图，在等腰梯形ABCD中，AD∥BC，BC=4AD=4，∠B=45°，直角三角板含45°角的顶点E在边 BC上移动，一直角边始终经过点A，斜边与CD交于点F，若△ABE为等腰三角形，则CF的长为______.

因为∠B＝∠AEF＝45°，而∠AEF＋∠FEC＝∠B＋∠BAE，所以∠FEC＝∠BAE，又根据等腰梯形的性质，可以知道，△ABE∽△ECF.并且根据等腰梯形已知边的长度，易计算边AB＝3.
如图，当BE＝AE时，因为∠B＝45°，根据等腰三角形的性质易知，∠BEA＝90°，即△ABE为等腰直角三角形，易计算BE＝，因此EC＝4－BE＝，根据三角形的相似性可以知道，△ECF也为等腰直角三角形，故易知CF＝.

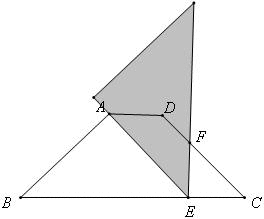
如图，当BE＝BA时，则BE＝BA＝3，且△ABE为等腰三角形，故EC＝4－3，再根据相似三角形的性质可以知道，CF＝EC＝4－3.

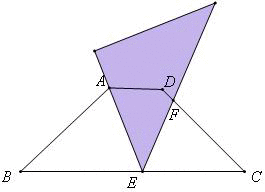
如图，当AB＝AE时，则△ABE为等腰直角三角形，且∠BAE＝90°，因此BE＝3，CE＝4－3＝，根据三角形的相似性，可以知道△ECD也为等腰直角三角形，且∠FEC＝90°，根据勾股定理可以知道，CF＝2.


 

对题中存在的各种情况考虑不全，不能将答案填完整.