如图，已知∠A=∠ABC，∠D=∠CBD，BD平分∠ABC，点E在BC的延长线上．
求证：CD平分∠ACE．


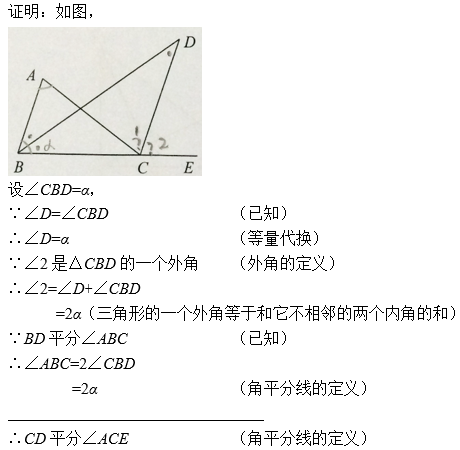
横线处应填写的过程，顺序正确的是(    )
①∵∠A=∠ABC（已知）
②∵∠ACE是△ABC的一个外角（外角的定义）
③∴∠1=∠2（等量代换）
④∴∠1=∠ACE-∠2
=2α（等式的性质）
⑤∴∠ACE=∠A+∠ABC
=2α+2α
=4α（三角形的一个外角等于和它不相邻的两个内角的和）
⑥∴∠A=2α（等量代换）
⑦∵AB∥CD（已知）
⑧∵∠ACD是△ABC的一个外角（外角的定义）

第一步：读题标注（见题目）；
第二步：走通思路；
要证CD平分∠ACE，只需证明∠1=∠2即可．
由∠D=∠CBD=α，根据外角定理，∠2=2α，
再利用角平分线的定义，得∠ABC=2α，
又因为∠A=∠ABC，得∠A=2α，接下来只需要证明∠1=2α即可；
把∠ACE看作△ABC的一个外角，
利用三角形的一个外角等于和它不相邻的两个内角的和，
得∠ACE=∠A+∠ABC=4α，
则∠1+∠2=4α，因此∠1=2α，等量代换，得∠1=∠2，
所以CD平分∠ACE．
第三步：规划过程；
根据分析，过程主要分为六个书写模块：
①利用设元法，设∠CBD=α，结合已知，等量代换，得∠D=α；
②利用三角形外角定理，得∠2 =2α；
③利用角平分线的定义，得∠ABC=2α；
④结合已知条件∠A=∠ABC，等量代换，得∠A=2α；
⑤利用三角形外角定理，得∠ACE=4α；
⑥最后利用等式的性质，得∠1=∠2．
故选B．

略