已知：如图，MN∥PQ，AB⊥PQ于点E，∠ABC=135°，则∠α=(    )

从已知出发，由MN∥PQ，要找同位角、内错角和同旁内角，
因此要找截线，若把DB当作截线（也可以把BA当截线），
如图，延长DB交PQ于点F，补全图形．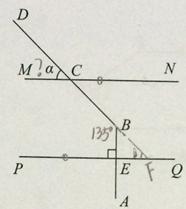

由MN∥PQ，利用平行线的性质，可得∠α=∠1，
因此只需要求∠1的度数即可；
由AB⊥PQ，得∠BEF=90°，
∠ABC是△BEF的一个外角，结合∠ABC=135°，利用外角定理，
得∠1=∠ABC-∠BEF=45°，所以∠α=∠1=45°．
故选D．

略