已知:如图,∠D=∠E,AM=ME=CN=DN.试猜想AB和BC的数量关系,并证明你的猜想.

解:AB=BC,理由如下:
如图,
在△BME和△BND中
∴△BME≌△BND( )
∴
∵AM=ME=CN=DN
∴AM+ME=CN+DN
即AE=CD
在△ABE和△CBD中
∴△ABE≌△CBD( )
∴AB=BC
请你仔细观察下列序号所代表的内容:
①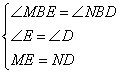 ;②
;②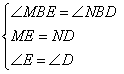 ;③ASA;④AAS;⑤SAS;⑥BE=BD;
;③ASA;④AAS;⑤SAS;⑥BE=BD;
⑦∠BME=∠BND;⑧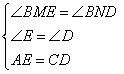 ;⑨
;⑨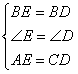 .
.
以上空缺处依次所填最恰当的是( )
- A.②③⑦⑧④
- B.②③⑥⑨⑤
- C.①④⑥⑨⑤
- D.①④⑦⑧④
答案
正确答案:C
知识点:全等三角形的性质 全等三角形的判定 全等三角形证明过程训练
结合图形猜测AB=BC.
观察图形,题中已知∠E=∠D,ME=DN,结合公共角∠MBE=∠NBD,
由AAS可得△BME≌△BND.
再观察图形,对比要证的结论AB=BC,可以把它们放在两个三角形中,
证△ABE≌△CBD.
由△BME≌△BND可得BE=BD,结合AM=ME=CN=DN可得AE=CD,
进而由SAS可得△ABE≌△CBD,因此AB=BC.
因此空缺处依次填写最恰当的是①④⑥⑨⑤.
故选C.
略








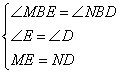 ;②
;②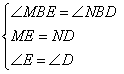 ;③ASA;④AAS;⑤SAS;⑥BE=BD;
;③ASA;④AAS;⑤SAS;⑥BE=BD;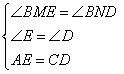 ;⑨
;⑨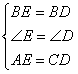 .
.