如图,在四边形ABCD,DEFG中,AD=CD,DE=DG,∠EDG=∠ADC=90°,连接CG交AD于N,连接AE交CG于M.
求证:AE=CG,AE⊥CG.
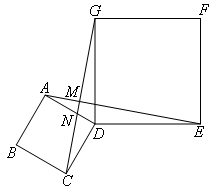
证明:如图,
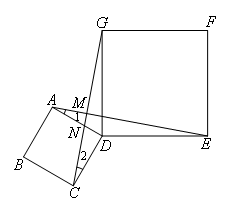
在△ADE和△CDG中
∴AE=CG
∠1=∠2
∵∠ADC=90°
∴∠2+∠CND=90°
∵∠ANM=∠CND
∴
∴∠AMN=90°
∴AE⊥CG
请你仔细观察下列序号所代表的内容:
①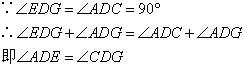 ;②
;②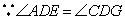 ;
;
③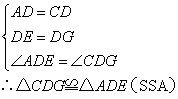 ;④
;④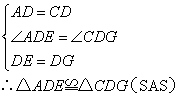 ;
;
⑤∠1+∠ANM=90°;⑥∠1+∠CND=90°.
以上空缺处依次所填最恰当的是( )
- A.①③⑥
- B.①④⑤
- C.②③⑤
- D.②④⑥
答案
正确答案:B
知识点:全等三角形的性质 全等三角形的判定 全等三角形证明过程训练
结合题中的已知条件,可以先证AE和CG相等,
考虑把这两条边分别放到△ADE和△CDG中证全等;
要证全等需要找三组条件,题目中已知AD=CD,DE=DG,
∠EDG=∠ADC,而且观察图形可知∠EDG和∠ADC分别加上公共
角∠ADG,可得∠ADE=∠CDG,用SAS可证△ADE≌△CDG,
由全等可得AE=CG,∠1=∠2;
结合题目中的条件∠ADC=90°,可知∠2+∠CND=90°,
又因为∠ANM=∠CND,所以∠1+∠ANM=90°,进而得到∠AMN=90°,
故有AE⊥CG.
因此空缺处依次填写最恰当的是①④⑤.
故选B.
略









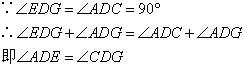 ;②
;②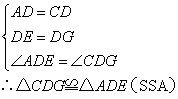 ;④
;④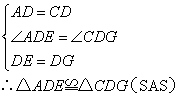 ;
;