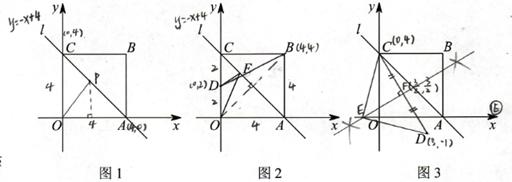
四边形OABC是边长为4的正方形，分别以OA，OC所在的直线为x轴，y轴，建立如图1所示的平面直角坐标系，直线l经过A，C两点．
（1）写出点A，点C的坐标并求直线l的函数表达式；
（2）若P是直线l上的一点，当△OPA的面积是5时，求出点P的坐标；
（3）如图2，若点D是OC的中点，E是直线l上的一个动点，求使OE+DE取得最小值时点E的坐标；
（4）如图3，点D(3，-1)，若E是x轴上的一个动点，则当ED=EC时，点E的坐标是        ；
（5）如图4，点D(3，-1)，若E是直线l上的一个动点，则|BE-DE|取得最大值时点E的坐标是        ，最大值是      ．

图1图2图3

图4

答案

（1）A(4，0)，C(0，4)，y=-x+4
（2）或
（3）
（4）(-1，0)
（5）(6，-2)，

知识点：轴对称——最值问题  

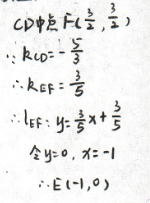
略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>