如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
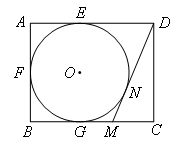
- A.
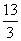
- B.
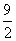
- C.
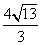
- D.
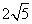
答案
正确答案:A
知识点:略
如图,连接OE,OF,OG,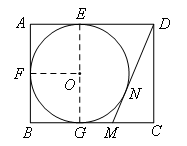
则OE=OF=OG,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠OFA=∠OEA=∠A=90°,∠OFB=∠OGB=∠B=90°,
∴四边形OEAF和四边形OFBG为正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
由切线长定理可得,DN=DE=3,MN=MG,
设MN=a,则DM=3+a,CM=3-a,
在Rt△DCM中,∠C=90°,CD=4,
由勾股定理得,(3-a)2+42=(3+a)2,
解得![]() ,
,
∴![]() .
.
略








