如图,Rt△ABC中,∠C=90°,∠B=30°,AB= ,点D在边BC上,且CD=2.点P是线段AD上一动点,当半径为
,点D在边BC上,且CD=2.点P是线段AD上一动点,当半径为 的⊙P与△ABC的一边相切时,PD的长为( )
的⊙P与△ABC的一边相切时,PD的长为( )

- A.2
- B.
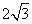
- C.
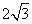 或2
或2 - D.
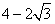 或2
或2
答案
正确答案:D
知识点:略
在Rt△ABC中,∠C=90°,∠B=30°,AB=![]() ,
,
∴AC=![]() ,BC=6,
,BC=6,
在Rt△ACD中,∠C=90°,CD=2,AC=![]() ,
,
由勾股定理得,AD=4,
∴∠CAD=30°.
①当⊙P与AC边相切,即点P到AC边的距离为![]() 时,
时,
如图所示,过点P作PE⊥AC于点E,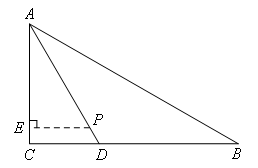
则![]() ,
,
在Rt△AEP中,∠AEP=90°,∠EAP=30°,![]() ,
,
∴![]() ,
,
∴![]() .
.
②当⊙P与AB边相切,即点P到AB边的距离为![]() 时,
时,
如图所示,过点P作PF⊥AB于点F,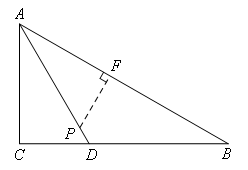
则![]() ,
,
在Rt△AFP中,∠AFP=90°,∠FAP=30°,![]() ,
,
∴![]() ,
,
∴![]() .
.
③当⊙P与BC边相切,即点P到BC边的距离为![]() 时,
时,
如图所示,过点P作PG⊥BC于点G,
则![]() ,
,
∵AC=![]() ,∠PGD=∠C=90°,
,∠PGD=∠C=90°,
易证PG为△ACD的中位线,
∴PD=2.
略








