（上接第4题）（2）如图2，若∠BCA=60°，α=120°，结论EF=BE-AF仍成立吗？若成立，请给出证明，若不成立，请说明理由.

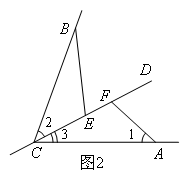
先在图上走通思路后再填写空格内容：
（2）由∠BCA=60°，∠AFC=120°，可以得到∠2+∠3=60°，∠3+∠1=60°，得到，理由是．又因为CB=AC，∠BEC=∠CFA，因此根据全等三角形的判定，可以得到，由全等的性质得CE=AF，BE=CF，所以EF=CF-CE=BE-AF．
请你仔细观察下列序号所代表的内容：
①∠2=∠3；②∠2=∠1；③等式性质；④同角或等角的余角相等；
⑤△BEC≌△AFC；⑥△BEC≌△CFA；⑦ASA；⑧AAS．
以上空缺处依次所填最恰当的是( )

答案

正确答案：B

本题与上一题条件相似，问法相同，判断是类比探究问题，
类比上一题，即（1）中的证明方法，把三角形全等的证明照搬到（2）中，
证得△BEC≌△CFA（AAS），
根据全等的性质，得到对应边的关系CE=AF，BE=CF，
进而推导出EF=BE-AF．
所以空缺处依次所填最恰当的是②③⑧⑥．
故选B．

略

下载次数：0