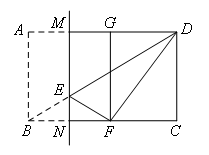
如图，在矩形ABCD中，AB:BC=3:5，点E是对角线BD上一动点（不与点B，D重合），将矩形沿过点E的直线MN折叠，使得点A，B的对应点G，F分别在直线AD与BC上．当△DEF为直角三角形时，CN:BN的值为____．

分析：分析背景图形，不变特征，D是定点，E，F是动点，∠DEF为固定的锐角，确定分类标准（∠DFE=90°或∠EDF=90°），作出相应的图形，利用三角函数值进行求解计算．
解答：
∵AB:BC=3:5
设AB=3x，BC=5x
∴CD=AB=3x，AD=BC=5x
1.如图所示，当∠DFE=90°时，△DEF为直角三角形

∵∠CDF+∠CFD=∠EFN+∠CFD=90°
∴∠CDF=∠EFN
由折叠可得，∠EFN=∠EBN
∴∠CDF=∠CBD
∵
∴
∴
∴
由折叠可知，
∴
∴
2.如图所示，当∠EDF=90°时，△DEF为直角三角形

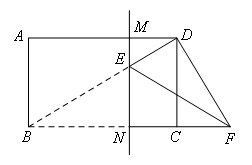
∵∠CDF+∠CFD=∠CBD+∠CFD=90°
∴∠CDF=∠CBD
∵CD=3x
∴
∴
∴
∴
∴
故填

略