已知函数y₁=x，y₂=-2x₂-m，若对∀x₁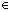{x|-1≤x≤3}，∃x₂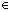{x|0≤x≤2}，使得y₁≥y₂，则实数m的取值范围为(    )

因为x₁{x|-1≤x≤3}，x₂{x|0≤x≤2}，
所以y₁{y|0≤y≤9}，y₂{y|-4-m≤y≤-m}，
又因为对∀x₁∈{x|-1≤x≤3}，∃x₂∈{x|0≤x≤2}，使得y₁≥y₂，
即y₁的最小值大于等于y₂的最小值，即-4-m≤0，所以m≥-4.故选D．

略