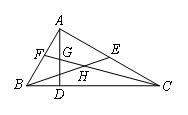
如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于G，交BE于H．下列结论：①S_△ABE=S_△BCE；②∠FAG=2∠ACF；③∠AFG=∠AGF；④BH=CH．其中一定正确的结论的序号是(    )

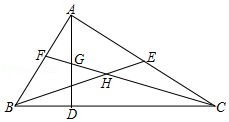
∵BE是中线，
∴AE=CE，
∴△ABE的面积=△BCE的面积（等底等高的三角形的面积相等），故①正确；
∵CF是角平分线，
∴∠ACF=∠BCF，
∵AD为高，
∴∠ADC=90°，
∵∠BAC=90°，
∴∠ABC+∠ACB=90°，∠ACB+∠CAD=90°，
∴∠ABC=∠CAD，
∵∠AFG=∠ABC+∠BCF，∠AGF=∠CAD+∠ACF，
∴∠AFG=∠AGF，故②正确；
∵AD为高，
∴∠ADB=90°，
∵∠BAC=90°，
∴∠ABC+∠ACB=90°，∠ABC+∠BAD=90°，
∴∠ACB=∠BAD，
∵CF是∠ACB的平分线，
∴∠ACB=2∠ACF，
∴∠BAD=2∠ACF，
即∠FAG=2∠ACF，故③正确；
根据已知条件不能推出∠HBC=∠HCB，即不能推出BH=CH，故④错误；

略