用正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形.
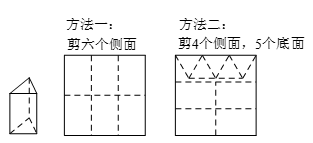
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
现有相同规格的19张正方形硬纸板,其中的x张按方法一裁剪,剩余的按方法二裁剪.
①用含x的代数式分别表示裁剪出的侧面个数,底面个数;
②若裁剪出的侧面和底面恰好全部用完,求能做多少个盒子.
答案
(1)3;2;
(2)①侧面个数:2x+76;底面个数:-5x+95;
②能做30个盒子.
解:(1)因为三棱柱盒子的侧面由3个矩形构成,底面都是三角形,所以每个盒子需3个长方形,2个等边三角形;
故答案是:3;2;
(2)裁剪时x张用方法一,
∴裁剪时(19﹣x)张用方法二.
∴侧面的个数为:6x+4(19﹣x)=(2x+76)个,
底面的个数为:5(19﹣x)=(95﹣5x)个;
(3)由题意,得(2x+76):(95﹣5x)=3:2,
解得:x=7,
∴盒子的个数为:![]() =30.
=30.
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
略








