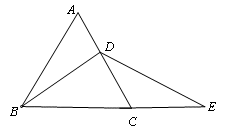
如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.求证:BD=DE.
答案
∵BD是正三角形ABC的AC边的中线,
∴BD⊥AC,BD平分∠ABC,∠DBE=30°.
∵CD=CE,
∴∠CDE=∠E.
∵∠ACE=120°,
∴∠CDE+∠E=60°.
∴∠CDE=∠E=30°.
∴BD=DE.
知识点:等边三角形的性质
欲证BD=DE,只需证∠DBE=∠E,根据等边三角形的性质及角的等量关系可证明∠DBE=∠E=30°.
对等腰三角形性质掌握不牢








