如图所示，平行四边形ABCD中，各内角的平分线分别相交于点E、F、G、H，求证：四边形EFGH是矩形.
证明：如图，
∵四边形ABCD是平行四边形
∴                              
∵AF与BH分别是∠BAD与∠ABC的平分线
∴                            
∴∠2+∠3=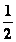（∠BAD+∠ABC）= 90°
∴∠AEB=90°
∴                            
同理，∠EHG=∠FGH=∠EFG=90°
∴四边形EFGH是矩形
下列选项填入以上空格，正确的是（）
①∠BAD+∠ABC=180°；②∠FEH=90°；③∠1=∠2，∠3=∠4.

• A.①③②
• B.①②③
• C.③①②
• D.③②①

答案

正确答案：A

知识点：特殊平行四边形的证明题规范书写  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>