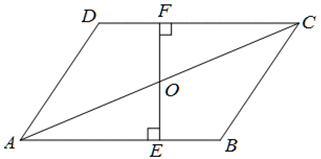
已知：如图，O是线段AC，FE的中点，OE⊥AB于E，OF⊥CD于F，DF=BE，求证：AD=BC.
答案
证明：如图，
∵OE⊥AB，OF⊥CD
∴∠AEO=∠CFO=90°
∵O是线段AC，FE的中点
∴AO=CO，OE=OF
在Rt△AEO和Rt△CFO中
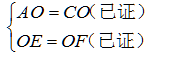
∴△AEO≌△CFO（HL）
∴AE=CF，∠OAE=∠OCF
∵DF=BE
∴DF+CF=BE+AE
即CD=AB
在△ADC和△CBA中
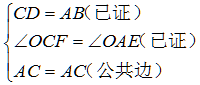
∴△ADC≌△CBA（SAS）
∴AD=BC
知识点：三角形全等
略
略
WORD格式（
