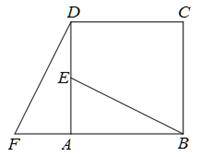
已知：如图，在正方形ABCD中，AB=AD，∠DAB=90°，E是AD中点，F是BA延长线上一点且AF=AE，试猜想线段BE与DF有怎样的数量和位置关系？并证明你的猜想.
答案
解：BE=DF，BE⊥DF
延长BE交DF于点G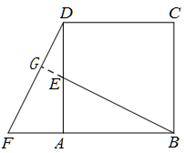
∵∠DAB=90°
∴∠FAD=90°
在Rt△ABE和Rt△ADF中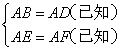
∴△ABE≌△ADF（HL）
∴BE=DF，∠ABE=∠ADF
∵∠DAB=90°
∴∠ABE+∠AEB=90°
∵∠AEB=∠DEG
∴∠ADF+∠DEG=90°
∴∠DGE=90°
∴BE⊥DF
知识点：三角形全等
略
略
WORD格式（
