已知：如图，△ABC中，AB=AC，∠BAC=90°，分别过B，C向过A的直线作垂线，垂足分别为E，F.
（1）如图1，过A的直线与斜边BC不相交时，求证：EF=BE+CF;
（2）如图2，过A的直线与斜边BC相交时，其他条件不变，若BE=10，CF=3，试求EF的长.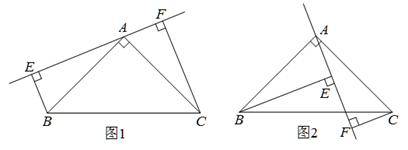

答案

证明：如图，
（1）由题意得：∠BEA=∠AFC=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC
在△EBA和△FAC中

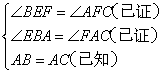
∴△EBA≌△FAC（AAS）
∴BE=AF，AE=CF
∵EF=AF+AE
∴EF=BE+CF
（2）由题意得：∠BEA=∠AFC=90°
∴∠EAB+∠EBA=90°
∵ ∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC
在△EBA和△FAC中

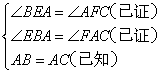
∴△EBA≌△FAC（AAS）
∴AE=CF，BE=AF
∵EF=AF-AE
∴EF=BE-CF
∵BE=10，CF=3
∴EF=7
即：EF的长为7.

知识点：三角形全等  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>