已知:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G,易证EG=EF.移动三角板,如图2,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,则此时EG与EF的大小关系是(    )

1．思路点拨
①辨识类型，这是一道类比探究题，那么就需要先搞清楚图1中是如何证明的，再把图1中的证明方法照搬过来.
②观察图1，要证明EG=EF，直接把EG和EF放到两个三角形中证全等即可，
即证明△EDF≌△EBG（ASA）；
③照搬图1中的证法来解决图2，需要把EG和EF放到两个三角形中，故需过点E分别向BC，CD边作垂线.
2．解题过程
如图，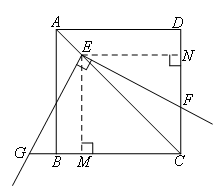

过点E分别作BC，CD边上的垂线，垂足为M，N，
∵CA平分∠BCD
∴EM=EN
∵∠GEM+∠MEF=90°，∠NEF+∠MEF=90°
∴∠GEM=∠NEF
在△EMG和△ENF中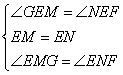

∴△EMG≌△ENF（ASA）
∴EG=EF.
故选B

略