如图,已知梯形ABCD,AD∥BC,AD=DC=4,BC=8,点N在BC上,CN=2,E是AB中点.在AC上找一点M使EM+MN的值最小,此时EM+MN的最小值为( )
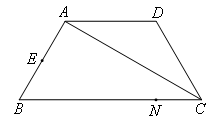
- A.6
- B.8
- C.4
- D.
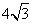
答案
正确答案:A
知识点:轴对称—最短路线问题
如图,
作点N关于AC的对称点![]() ,连接
,连接![]() 交AC于M,连接MN,此时EM+MN的值最小.
交AC于M,连接MN,此时EM+MN的值最小.
∵AD∥BC,AD=DC=4,
∴∠DAC=∠ACB,∠DAC=∠DCA,
∴∠ACB=∠DCA,
∴点N关于AC的对称点![]() 在CD上,
在CD上,![]() .
.
又∵DC=4,
∴![]() 为CD中点,
为CD中点,
∴![]() 为梯形ABCD的中位线,
为梯形ABCD的中位线,
∴![]() ,
,
∴EM+MN最小值为![]() .
.
略








