阅读下面材料：
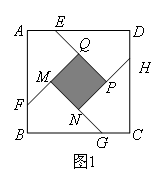
小明遇到这样一个问题：如图1，在边长为a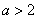（）的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积．
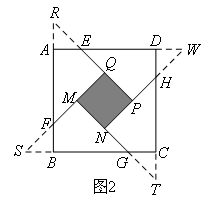
小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形，如图2．
请回答：
（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙不重叠），则这个新正方形的边长及正方形MNPQ的面积分别为( )

A.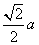，4
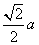B.，2
C.a，4
D.a，2

答案

正确答案：D

∵四边形ABCD为正方形，
∴∠BAD=∠RAE=90°．
∵△RQF为等腰直角三角形，
∴∠ARE=45°，
∴∠AER=45°，即△RAE为等腰直角三角形，
∴AR=AE=1．
又∵BF=AE=1，
∴FR=FA+AR=FA+BF=AB=a，
即新正方形的边长为a．
同理可得△SBF，△TCG，△WDH均是直角边长为1的等腰直角三角形．
∵四个等腰直角三角形的面积和即新正方形的面积为，
正方形ABCD的面积为，
∴．

略

下载次数：0

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>