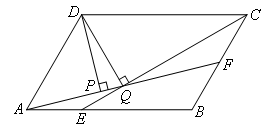
如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,
F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )
- A.3:4
- B.
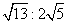
- C.
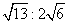
- D.
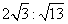
答案
正确答案:D
如图,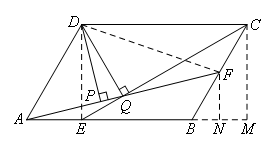
连接DE,DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
根据题意得,![]() ,
,
即![]() ,
,
∴![]() .
.
设AB=3a,则AE=BF=a,EB=BC=2a,
易得∠DAE=∠CBM=60°,
∴∠BFN=∠BCM=30°,
∴在Rt△BFN和Rt△BCM中,![]() ,
,
∴![]() .
.
在Rt△ANF和Rt△ECM中应用勾股定理得,![]() ,
,
∴![]() ,
,
∴![]() .
.
故选D.
略








