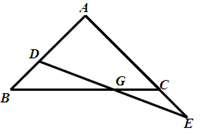
在△ABC中，AB=AC，在AB上取点D，在AC延长线上取点E，使CE=BD，连接DE，交BC于点G.
求证：DG=GE.
答案
证明：
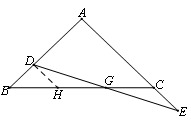
过D作DH∥AC交BC于点H，
∵AB=AC，∴∠ABC=∠ACB=∠DHB，
∴DB=DH=CE，
又∵∠HDG=∠CEG，∠DGH=∠CGE，
∴△DHG≌△ECG
∴DG=GE
知识点：全等三角形的判定
过点D作DH∥AC交BC于点H，根据等腰三角形的性质可以知道BD＝DH＝CE，进而可以证明△DHG≌△ECG，则结论即可证明。
找合适的辅助线；全等三角形的判定
WORD格式（
