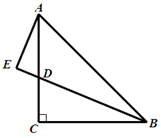
如图,在△ABC中,AC=BC,
∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于点E,且BD=2AE.求证:BD是∠ABC的
角平分线.
答案
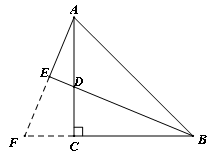
延长BC、AE交于点F.∵AC⊥BC于点C,AE⊥BD于E,
∴∠AED=90°,∠ACB=90°,
∴∠EAD+∠ADE=90°,∠CDB+∠CBD=90°.
又∠ADE=∠CDB,∴∠EAD =∠CBD.
又∵AC=CB,∴Rt△ACF≌Rt△BCD(ASA),
∴AF=BD=2AE,∴AE=EF,即E为AF的中点.
又∵AE⊥BE,∴△ABE≌△FBE(SAS),
∴∠ABE=∠FBE,即BD是∠ABC的角平分线
知识点:全等三角形的判定
延长BC、AE交于点F,由已知条件AC⊥BC,AE⊥BD可知,∠EAD+∠ADE=90°,∠CDB+∠CBD=90°,又根据已知的条件∠ADE=∠CDB知,∠EAD =∠CBD,则易证Rt△ACF≌Rt△BCD,因此可知E为AF的中点,则可易证△ABE≌△FBE,结论即证。
找合适的辅助线;直角三角形全等的判定








