如图，在四边形ABCD中，AB∥CD，E为BC边的中点，∠1=∠2，下列结论正确的是(    )

如图，在四边形ABCD中，AD∥BC，E为AB边的中点，G，F分别为AD，BC边上的点，
GE⊥EF，若AG=2，BF=3，则GF=(    )

如图，已知AD是△ABC的中线，∠ADB，∠ADC的平分线分别交AB于点E，交AC于点F．则BE+CF与EF的大小关系是(    )

如图，点E是BC的中点，∠BAE＝∠D．某同学通过添加辅助线：延长DE到点F，使
EF=DE，连接BF．给出下列结论：①△BFE≌△CDE，②BF∥CD，③AB=CD，④AE=BE，其中一定正确的有(    )

如图，在四边形ABCD中，AD∥BC，E为AB边的中点，G，F分别为AD，BC边上的点，
GE⊥EF，若AG=2，BF=3，则GF=(    )

已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，
求证：∠C=∠BAE．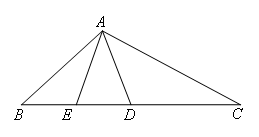

证明：如图，                            ．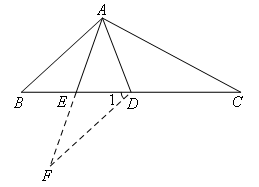

∵AE是△ABD的中线
∴BE=ED
在△ABE和△FDE中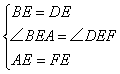

∴△ABE≌△FDE（SAS）
∴                            
∵CD=AB
∴CD=FD
∵∠ADF=∠ADB+∠1
∴∠ADF=∠ADB+∠B
∵∠ADC为△ABD的一个外角
∴∠ADC=∠B+∠BAD
∵∠ADB=∠BAD
∴∠ADF=∠ADC
在△FAD和△CAD中

∴△FAD≌△CAD（SAS）
∴                            
∴∠C=∠BAE
请你仔细观察下列序号所代表的内容：
①延长AE到F，连接DF，使得DF∥AB；
②延长AE到F，使得EF=AE，连接DF；
③延长AE到F，使得EF=AE，连接DF，过D作DF∥AB；
④AB=FD，AE=EF；
⑤AB=FD，∠BAE=∠F，∠B=∠1；
⑥AB=FD；
⑦AF=AC；
⑧∠F=∠C．
以上空缺处依次所填最恰当的是(    )

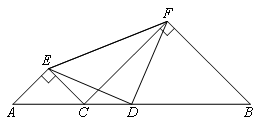
已知：如图，D为线段AB的中点，在AB上任取一点C（不与点A，B，D重合），
分别以AC，BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF，∠AEC=∠CFB=90°，AE=CE，CF=BF，
连接DE，DF，EF．
求证：DE⊥DF．

先在图上走通思路后再填写空格内容：
①因为点D是AB的中点，考虑                                          （叙述辅助线）；
②倍长之后先证明       ≌       ，理由是       ，由全等的性质得         ，为接下来的全等准备条件；
③结合已知条件∠AEC=∠CFB=90°，AE=CE，CF=BF，经过推理得CE=BG，∠ECF=∠GBF=90°，因此可以证明       ≌       ，理由是       ，由全等的性质得         ；
④△EFG是等腰三角形，且D为底边EG的中点，根据                         ，得DE⊥DF．
以上空缺处依次所填最恰当的是(    )

如图，在四边形ABCD中，AD∥BC，M是CD的中点，若AB=AD+BC，∠ABC=50°，则∠BAM=(    )

如图，已知AD是△ABC的中线，∠ADB，∠ADC的平分线分别交AB于点E，交AC于点F．则BE+CF与EF的大小关系是(    )

已知：如图，AD是△ABC的中线，E是AD上一点，BE的延长线交AC于点F，
∠AEF=∠FAE．
求证：BE=AC．


请你仔细观察下列序号所代表的内容：
①延长AD到点H，使AD=DH，连接CH；
②延长AD到点H，使DH=AD，连接BH；
③延长AD到点H，使DH=AD，过B作BH∥AC；
④；⑤．
以上空缺处依次所填最恰当的是(    )